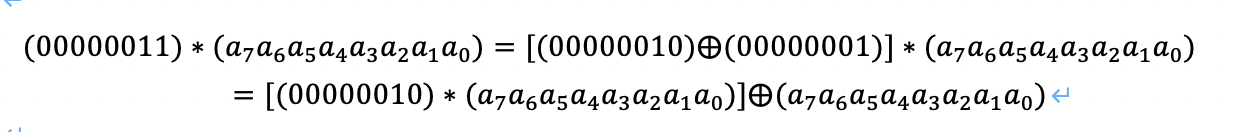对称密码
密码编码学分为:对称密码学,非对称密码学,密码协议。
对称加密方案也称为对称密钥(Symmetric-key)、秘密密钥(secret-key)、和单密钥(Single-key)算法,对称加密分为:分组密码和序列密码
对称加密算法的加密密钥和解密密钥是完全相同的,第一,加密算法必须足够强,第二,加密的安全性依赖于密钥的秘密性,而非算法的保密性。
假设用对称加密算法检验注册码,正确的方法是吧用户输入的注册码作为加密算法或解密算法的密钥,这样,解密者想要找到一个正确的注册码,只能穷举。但如果在检查注册码是,将用户的输入的采用做算法的输入输出,则无论是使用加密算法还是解密,解密者都可以利用调试器在内存中找到所用的密钥中,从而将算法求逆,写出注册机。
常见的对称分组加密有DES,IDEA,AES,BlowFish,TowFish,TEA,RC4等等,以下介绍几例
分组加密
分组加密叫块加密,
分组密码有五种工作体制:1.电码本模式(Electronic Codebook Book (ECB));2.密码分组链接模式(Cipher Block Chaining (CBC));3.计算器模式(Counter (CTR));4.密码反馈模式(Cipher FeedBack (CFB));5.输出反馈模式(Output FeedBack (OFB))。
序列加密
IDEA
密钥长度128bit,分组长度64bit,由James Massey与来学嘉设计,在1991年首次提出。
现在IDEA被认为是不安全的加密算法
加密步骤
1.生成子密钥
IDEA共有52个16位子密钥,该密钥由输入的128位密钥生成
- 输入的128位被分为8个16位分组,并直接作为前8个子密钥使用
- 128位密钥循环左移25位,生成的128位密钥被分成8个16位的分组,作为接下来的8个密钥
- 重复上一步,直至52个子密钥全部生成
IDEA算法的加密过程
分析IDEAKeyGenMe
使用FindCrypt查看 加密为RIPEMD160和SHA1和SHA1加密一样啊
TEA
TEA算法是分组密码,分组长度为64位,密钥长度为128位,采用Feistel网络。
加密过程
#include <stdint.h>
void encrypt (uint32_t v[2], const uint32_t k[4]) {
uint32_t v0=v[0], v1=v[1], sum=0, i;
uint32_t delta=0x9E3779B9;
uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3];
for (i=0; i<32; i++) {
sum += delta;
v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
}
v[0]=v0; v[1]=v1;
}
|
其中特征常量delta是由黄金分割点得来的,delta = 0x9E377989。TEA的变体XTEA和XXTEA都用到了这个常量,但是加密过程不同,在识别算法时需要注意。
在加密轮数方面,作者推荐的加密轮数是64轮,即循环32次,也可以采用其他加密轮数,比如32轮或者128轮,在分析的时候也需要注意。
DES
密钥长64位,56位参与运算,8位校验(每八位的第八位)
现在DES被认为是不安全的
当n个64位明文数据参与运算经过DES处理,
加密方法
IP初始置换 –》16轮迭代 –》IP-1逆置换
将64位化为两部分L0和R0(都是32位)
R1=L0^f(R0,K1)
以下对上述过程解释:
IP置换:ip置换,ip的表将对应位置的原始数据
16轮迭代分为F轮函数和异或,F轮函数分为:1.E扩展,2.异或,3.S盒,4.P置换
1.E扩展:右32bit转化为48位
S盒压缩处理:分为8个6bit的字符,将6位压缩为4位输出 48-》32(根据一个6进4出的S盒 )
P置换和ip置换差不多
P置换后要和L0进行异或得到R0
逆置换和ip置换差不多
AES
明文固定长度128位,密钥长度可以是128,192,256位
AES成为最流行的算法之一,已有破解方法
加密方法
明文 –> 初始变换 –> 9轮循环运算 –> 1轮最终轮 –> 密文
循环运算:1.字节代换,2.行位移,3.列混合,4.轮密钥加;最终轮无3
下面对上面的加密过程进行解释;
1.初始变换:将明文划为16字节(4*4矩阵),和密钥进行异或
2.1字节代换:矩阵在S盒中找到相应的位置进行代换
2.2行位移:第一行位置不变,第二行向左位移1位,第三行向左位移2位,向左位移3位
2.3列混合:将输入的 (4*4) 矩阵左乘一个 4*4给定的矩阵
正矩阵(好像一般是这个)
2|3|1|1
1|2|3|1
1|1|2|3
3|1|1|2
|
2.4轮密钥加:将结果和子密钥进行异或
子密钥如何得到呢?初始密钥经过密钥扩展可得到10个子密钥
密钥扩展:设有个密钥为4*4的矩阵W,i为列数
1.如果说i不是4的倍数,W[i]=W[i-1]^W[i-4]
2.如果是i的倍数,W[i]=W[i-4]^T(W[i-1])
T函数包含:字循环,字节代换和轮常量异或
字循环:将i-1列的第一个放在最后一个
字节代换:将循环结果查看S盒进行代换
轮常量异或:轮常量是给定的,将前两步得到的结果和轮常量进行异或即可
其中,矩阵元素的乘法和加法都是定义在基于GF(2^8)上的二元运算,并不是通常意义上的乘法和加法。这里涉及到一些信息安全上的数学知识,不过不懂这些知识也行。其实这种二元运算的加法等价于两个字节的异或,乘法则复杂一点。对于一个8位的二进制数来说,使用域上的乘法乘以(00000010)等价于左移1位(低位补0)后,再根据情况同(00011011)进行异或运算,设S1 = (a7 a6 a5 a4 a3 a2 a1 a0),刚0x02 * S1如下图所示:

也就是说,如果a7为1,则进行异或运算,否则不进行。
类似地,乘以(00000100)可以拆分成两次乘以(00000010)的运算:

乘以(0000 0011)可以拆分成先分别乘以(0000 0001)和(0000 0010),再将两个乘积异或:

因此,我们只需要实现乘以2的函数,其他数值的乘法都可以通过组合来实现。
解密方法
对称加密加解密使用一套算法,只是用逆变换取代原来的变换。
算法实现
AES有五种加密模式(CBC、ECB、CTR、OCF、CFB),以下算法为ECB
AES加密函数中,首先进行密钥扩展,然后把128位长度的字符串读进一个4*4的整数数组中,这个数组就是状态矩阵。例如,pArray[0][0] = S0,pArray[1][0] = S1, pArray[0][1] = S4。这个读取过程是通过 convertToIntArray()函数来实现的。每个轮操作的函数都对pArray进行修改,也就是对状态矩阵进行混淆。在执行完10轮加密后,会把pArray转换回字符串,再存入明文p的字符数组中,所以,在加密完后,明文p的字符串中的字符就是加密后的字符了。这个转换过程是通过convertArrayToStr()函数来实现的。
void aes(char *p, int plen, char *key){
int keylen = strlen(key);
if(plen == 0 || plen % 16 != 0) {
printf("明文字符长度必须为16的倍数!\n");
exit(0);
}
if(!checkKeyLen(keylen)) {
printf("密钥字符长度错误!长度必须为16、24和32。当前长度为%d\n",keylen);
exit(0);
}
extendKey(key);
int pArray[4][4];
for(int k = 0; k < plen; k += 16) {
convertToIntArray(p + k, pArray);
addRoundKey(pArray, 0);
for(int i = 1; i < 10; i++){
subBytes(pArray);
shiftRows(pArray);
mixColumns(pArray);
addRoundKey(pArray, i);
}
subBytes(pArray);
shiftRows(pArray);
addRoundKey(pArray, 10);
convertArrayToStr(pArray, p + k);
}
}
|
密钥扩展
static int w[44];
static void extendKey(char *key) {
for(int i = 0; i < 4; i++)
w[i] = getWordFromStr(key + i * 4);
for(int i = 4, j = 0; i < 44; i++) {
if( i % 4 == 0) {
w[i] = w[i - 4] ^ T(w[i - 1], j);
j++;
}else {
w[i] = w[i - 4] ^ w[i - 1];
}
}
}
|
T函数实现
static const int Rcon[10] = { 0x01000000, 0x02000000,
0x04000000, 0x08000000,
0x10000000, 0x20000000,
0x40000000, 0x80000000,
0x1b000000, 0x36000000 };
static int T(int num, int round) {
int numArray[4];
splitIntToArray(num, numArray);
leftLoop4int(numArray, 1);
for(int i = 0; i < 4; i++)
numArray[i] = getNumFromSBox(numArray[i]);
int result = mergeArrayToInt(numArray);
return result ^ Rcon[round];
}
|
代码代换
static int getNumFromSBox(int index) {
int row = getLeft4Bit(index);
int col = getRight4Bit(index);
return S[row][col];
}
static void subBytes(int array[4][4]){
for(int i = 0; i < 4; i++)
for(int j = 0; j < 4; j++)
array[i][j] = getNumFromSBox(array[i][j]);
}
|
行移位
static void leftLoop4int(int array[4], int step) {
int temp[4];
for(int i = 0; i < 4; i++)
temp[i] = array[i];
int index = step % 4 == 0 ? 0 : step % 4;
for(int i = 0; i < 4; i++){
array[i] = temp[index];
index++;
index = index % 4;
}
}
static void shiftRows(int array[4][4]) {
int rowTwo[4], rowThree[4], rowFour[4];
for(int i = 0; i < 4; i++) {
rowTwo[i] = array[1][i];
rowThree[i] = array[2][i];
rowFour[i] = array[3][i];
}
leftLoop4int(rowTwo, 1);
leftLoop4int(rowThree, 2);
leftLoop4int(rowFour, 3);
for(int i = 0; i < 4; i++) {
array[1][i] = rowTwo[i];
array[2][i] = rowThree[i];
array[3][i] = rowFour[i];
}
}
|
列混合
static const int colM[4][4] = { 2, 3, 1, 1,
1, 2, 3, 1,
1, 1, 2, 3,
3, 1, 1, 2 };
static int GFMul2(int s) {
int result = s << 1;
int a7 = result & 0x00000100;
if(a7 != 0) {
result = result & 0x000000ff;
result = result ^ 0x1b;
}
return result;
}
static int GFMul3(int s) {
return GFMul2(s) ^ s;
}
static int GFMul(int n, int s) {
int result;
if(n == 1)
result = s;
else if(n == 2)
result = GFMul2(s);
else if(n == 3)
result = GFMul3(s);
else if(n == 0x9)
result = GFMul9(s);
else if(n == 0xb)
result = GFMul11(s);
else if(n == 0xd)
result = GFMul13(s);
else if(n == 0xe)
result = GFMul14(s);
return result;
}
static void mixColumns(int array[4][4]) {
int tempArray[4][4];
for(int i = 0; i < 4; i++)
for(int j = 0; j < 4; j++)
tempArray[i][j] = array[i][j];
for(int i = 0; i < 4; i++)
for(int j = 0; j < 4; j++){
array[i][j] = GFMul(colM[i][0],tempArray[0][j]) ^ GFMul(colM[i][1],tempArray[1][j])
^ GFMul(colM[i][2],tempArray[2][j]) ^ GFMul(colM[i][3], tempArray[3][j]);
}
}
|
轮密钥加
static void addRoundKey(int array[4][4], int round) {
int warray[4];
for(int i = 0; i < 4; i++) {
splitIntToArray(w[ round * 4 + i], warray);
for(int j = 0; j < 4; j++) {
array[j][i] = array[j][i] ^ warray[j];
}
}
}
|
AES解密
void deAes(char *c, int clen, char *key) {
int keylen = strlen(key);
if(clen == 0 || clen % 16 != 0) {
printf("密文字符长度必须为16的倍数!现在的长度为%d\n",clen);
exit(0);
}
if(!checkKeyLen(keylen)) {
printf("密钥字符长度错误!长度必须为16、24和32。当前长度为%d\n",keylen);
exit(0);
}
extendKey(key);
int cArray[4][4];
for(int k = 0; k < clen; k += 16) {
convertToIntArray(c + k, cArray);
addRoundKey(cArray, 10);
int wArray[4][4];
for(int i = 9; i >= 1; i--) {
deSubBytes(cArray);
deShiftRows(cArray);
deMixColumns(cArray);
getArrayFrom4W(i, wArray);
deMixColumns(wArray);
addRoundTowArray(cArray, wArray);
}
deSubBytes(cArray);
deShiftRows(cArray);
addRoundKey(cArray, 0);
convertArrayToStr(cArray, c + k);
}
}
|
参考链接
《加密与解密》 作者段钢 6.2对称加密算法
hash加密
AES加密
AES的五种加密模式